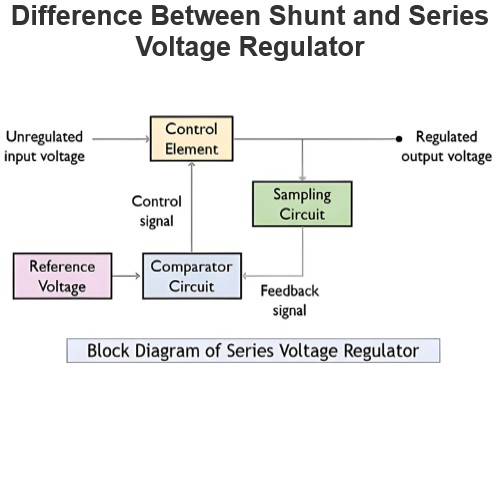
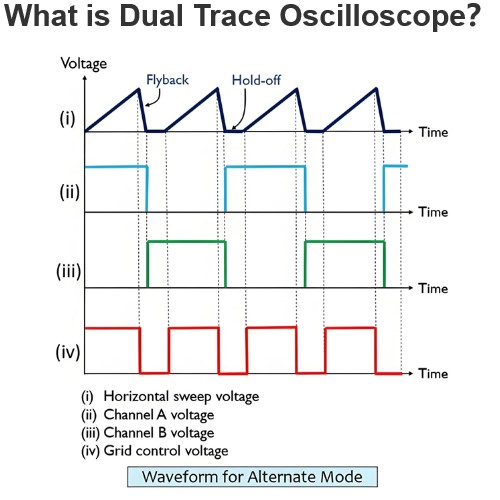
Network Synthesis | Hurwitz Polynomial | Positive Real Functions

Theory of Network Synthesis
Network Functions
Network synthesis theory involves the synthesis of networks made up of both active components (like resistors) and passive components (like inductors and capacitors).
Let’s start with the basics: what is a network function? In the frequency domain, network functions are defined as the quotient obtained by dividing the phasor corresponding to the circuit output by the phasor corresponding to the circuit input.
In simple words, network functions are the ratio of output phasor to the input phasor when phasors exist in the frequency domain. The general form of network functions is given below:
Now with the help of the above general network function, we can describe the necessary conditions for the stability of all the network functions. There are three mains necessary conditions for the stability of these network functions and they are written below:
The degree of the numerator of F(s) should not exceed the degree of denominator by more than unity. In other words (m – n) should be less than or equal to one.
F(s) should not have multiple poles on the jω-axis or the y-axis of the pole-zero plot.
F(s) should not have poles on the right half of the s-plane.
Hurwitz Polynomial
If above all the stability criteria are fulfilled (i.e. we have stable network function) then the denominator of the F(s) is called the Hurwitz polynomial.
Where, Q(s) is a Hurwitz polynomial.
Properties of Hurwitz Polynomials
There are five important properties of Hurwitz polynomials and they are written below:
For all real values of s value of the function P(s) should be real.
The real part of every root should be either zero or negative.
Let us consider the coefficients of denominator of F(s) is bn, b(n-1), b(n-2). . . . b0. Here it should be noted that bn, b(n-1), b0 must be positive and bn and b(n-1) should not be equal to zero simultaneously.
The continued fraction expansion of even to the odd part of the Hurwitz polynomial should give all positive quotient terms, if even degree is higher or the continued fraction expansion of odd to the even part of the Hurwitz polynomial should give all positive quotient terms, if odd degree is higher.
In case of purely even or purely odd polynomial, we must do continued fraction with the of derivative of the purely even or purely odd polynomial and rest of the procedure is same as mentioned in the point number (4).
From the above discussion we conclude one very simple result, If all the coefficients of the quadratic polynomial are real and positive then that quadratic polynomial is always a Hurwitz polynomial.
Positive Real Functions
Any function which is in the form of F(s) will be called as a positive real function if fulfill these four important conditions:
F(s) should give real values for all real values of s.
P(s) should be a Hurwitz polynomial.
If we substitute s = jω then on separating the real and imaginary parts, the real part of the function should be greater than or equal to zero, means it should be non negative. This most important condition and we will frequently use this condition in order to find out the whether the function is positive real or not.
On substituting s = jω, F(s) should posses simple poles and the residues should be real and positive.
Properties of Positive Real Function
There are four very important properties of positive real functions and they are written below:
Both the numerator and denominator of F(s) should be Hurwitz polynomials.
The degree of the numerator of F(s) should not exceed the degree of denominator by more than unity. In other words (m-n) should be less than or equal to one.
If F(s) is positive real function then reciprocal of F(s) should also be positive real function.
Remember the summation of two or more positive real function is also a positive real function but in case of the difference it may or may not be positive real function.
Following are the four necessary but not the sufficient conditions for the functions to be a positive real function and they are written below:
The coefficient of the polynomial must be real and positive.
The degree of the numerator of F(s) should not exceed the degree of denominator by more than unity. In other words (m – n) should be less than or equal to one.
Poles and zeros on the imaginary axis should be simple.
Let us consider the coefficients of denominator of F(s) is bn, b(n-1), b(n-2). . . . b0.Here it should be noted that bn, b(n-1), b0 must be positive and bn and b(n-1) should not be equal to zero simultaneously.
Now there two necessary and sufficient conditions for the functions to be a positive real function and they are written below:
F(s) should have simple poles on the jω axis and the residues of these poles must be real and positive.
Summation of both numerator and denominator of F(s) must be a Hurwitz polynomial.
Statement: Respect the original, good articles worth sharing, if there is infringement please contact delete.
Electrical4U is dedicated to the teaching and sharing of all things related to electrical and electronics engineering.