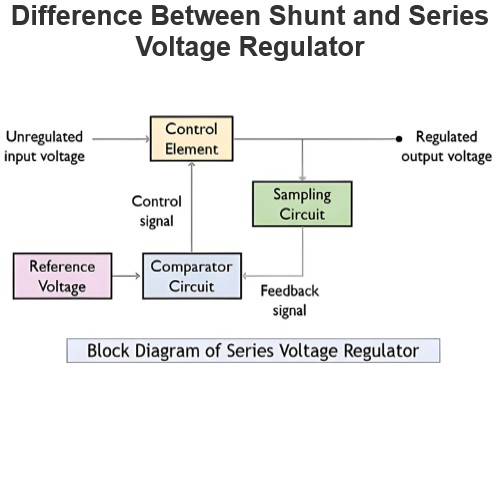
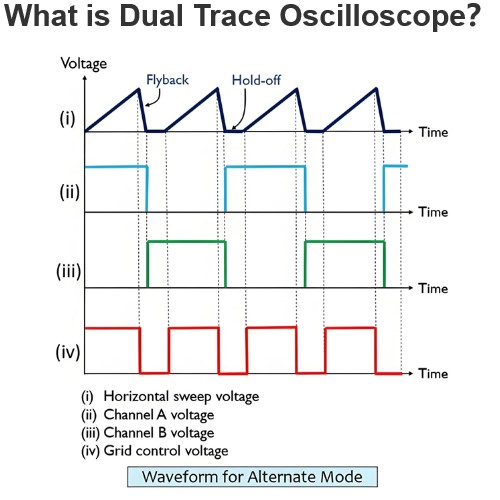
Final Value Theorem in Laplace Transform (Proof & Examples)

In the solution of Networks, Transient, and Systems sometimes we may not be interested in finding out the entire function of time f(t) from it’s Laplace Transform F(s), which is available for the solution. It is very interesting to find that we can find the first value or last value of f(t) or it’s derivatives without having to find out the entire function f(t). We will be interested in finding out final values and it’s derivatives in this article.

For the sake of example:
If F(s) is given, we would like to know what is F(∞), Without knowing the function f(t), which is Inverse Laplace Transformation, at time t→ ∞. This can be done by using the property of Laplace Transform known as Final Value Theorem. Final value theorem and initial value theorem are together called the Limiting Theorems.

Definition of Final Value Theorem of Laplace Transform

If f(t) and f'(t) both are Laplace Transformable and sF(s) has no pole in jw axis and in the R.H.P. (Right half Plane) then,

Proof of Final Value Theorem of Laplace Transform
We know differentiation property of Laplace Transformation:

Note
Here the limit 0– is taken to take care of the impulses present at t = 0
Now we take limit as s → 0. Then e-st → 1 and the whole equation looks like

Examples of Final Value Theorem of Laplace Transform
Find the final values of the given F(s) without calculating explicitly f(t)

Answer


Answer

Note
See here Inverse Laplace Transform is difficult in this case. Still we can find the Final Value through the Theorem.

Answer
Note
In Example 1 and 2 we have checked the conditions too but it satisfies them all. So we refrain ourselves of showing explicitly. But here the sF(s) has a pole on the R.H.P as the denominator have a positive root.
So, here we can’t apply Final Value Theorem.

Answer
Note
In this example sF(s) has poles on jw axis. +2i and -2i specifically.
So, here we can’t apply Final Value Theorem as well.

Answer
Note

Points to remember:

• For applying FVT we need to ensure that f(t) and f'(t) are transformable.

• We need to ensure that the Final Value exists. Final value doesn’t exist in the following cases

If sF(s) has poles on the right side of s plane. [Example 3]
If sF(s) has conjugate poles on jw axis. [Example 4]
If sF(s) has pole on origin. [Example 5]

• Then apply

In this example sF(s) has pole on the origin.
So here we can’t apply Final Value Theorem as well.
Final Trick
Just check that sF(s) is unbounded or not. If unbounded, then it is not fit for Final Value Theorem and the final value is simply infinite.

Statement: Respect the original, good articles worth sharing, if there is infringement please contact delete.